La Passione e la Sindone

I parametri del modello

I 700 coefficienti definiti dagli autori, relativi alle 100 affermazioni sopra considerate, sono stati inseriti in un software appositamente scritto in linguaggio per il “Mathcad 7”. Il software parte dalla definizione di 7 vettori (a, f, n, ia, if, in, p) di cui i primi tre in riferimento alla probabilità che sia verificata l’alternativa A, F oppure N, i secondi tre in riferimento alle corrispondenti incertezze nell’assegnazione delle probabilità ed infine un peso assegnato in relazione all’importanza dell’affermazione.
Si sono quindi ottenuti i seguenti risultati:

• • alternativa A (autentica) : probabilità del 100% e incertezza pari a 10-83
  
• • alternativa F (falsa, medievale o post-medievale): probabilità dello 0% e incertezza pari a 10 -183
  
• • alternativa N (non autentica, né falsa medievale o post-medievale): probabilità dello 0% e incertezza pari a 10-83
  

Si può pensare all’analogia con il gioco della roulette: la probabilità che esca il numero 36 dopo una giocata è 1/37 (esistono tutte le possibilità tra lo zero ed il numero 36; la probabilità che esca dieci volte consecutive il numero 36 è 1/3710 cioè un uno diviso un numero con 15 zeri). In riferimento alla probabilità che si verifichino le alternative A, F oppure N, equivale ad affermare che è più probabile fare uscire:

• • per 116 volte consecutive uno stesso numero al gioco della roulette piuttosto che affermare che la ST sia falsa, medievale o post-medievale.
  
• • per 52 volte consecutive uno stesso numero al gioco della roulette piuttosto che affermare che la ST non sia né autentica né falsa, medievale o post-medievale.

A questo punto si ritiene necessaria una verifica di stabilità del risultato anche in seguito alle ipotesi fatte nel modello. Per questo motivo si considerano i seguenti casi:

• • il settimo parametro, peso, introdotto nel modello per differenziare l’attendibilità delle diverse affermazioni, le rende implicitamente dipendenti. Per eliminare la dipendenza si pone in questo caso il peso pari a 1
  
• • le affermazioni relative alle Sacre Scritture (n°83-100) possono introdurre una dipendenza e non essere accettate, per cui in esse si è posto il peso pari a 0
  
• • nell’ipotesi che da un punto di vista estremamente critico vengano discusse le affermazioni n° 2, 7, 13, 15, 16, 17, 22, 23, 24, 28, 30, 36, 37, 56, si assegna un peso pari a 0 a tali affermazioni.
  

• Si riportano in Tabella i risultati ottenuti dal programma di calcolo

  

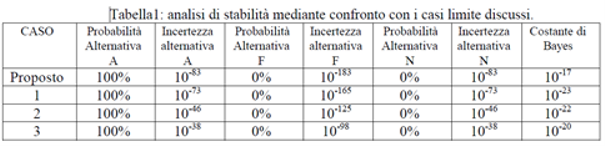
Dai risultati indicati in Tabella 1 non sembra opportuna alcuna discussione sulla probabilità dell’alternativa A che in ogni caso è del 100% con incertezza infinitesima. Per ottenere risultati di alternative non mutuamente escludentisi, in riferimento ad altri modelli probabilistici, si dovrebbe moltiplicare la probabilità ottenuta per la costante di Bayes nei casi sopra esaminati.

Conclusioni

È stato applicato un modello probabilistico, sviluppato dagli stessi autori in un altro lavoro, a 100 affermazioni risultanti dalle ricerche finora eseguite sulla Sindone di Torino.  Sono state definite tre diverse possibili alternative riguardanti l’origine della ST: l’alternativa A (autentica) afferma che la ST abbia avvolto il corpo di Gesù, l’alternativa F (falsa) afferma che la ST è di origine medievale, mentre l’alternativa N (non autentica, ma nemmeno falsa medievale) considera tutte le altre possibili origini, non escluso il miracolo.

 A ciascuna affermazione sono stati assegnati 7 coefficienti di cui i primi tre in riferimento alla probabilità che sia verificata l’alternativa A, F oppure N, i secondi tre in riferimento alle corrispondenti incertezze nell’assegnazione delle probabilità ed infine un peso assegnato in relazione all’importanza dell’affermazione. I 700 coefficienti assegnati dagli autori alle 100 affermazioni sono stati inseriti nel modello probabilistico per definire il grado di attendibilità delle tre diverse alternative.

 Risulta che la ST è autentica con probabilità del 100% e corrispondente incertezza pari a 10^-83; l’alternativa F ha una probabilità dello 0% e corrispondente incertezza pari a 10^-183, l’alternativa N ha una probabilità dello 0% e corrispondente incertezza pari a 10^-83. Ciò equivale ad affermare che è più probabile fare uscire per 52 volte consecutive uno stesso numero al gioco della roulette piuttosto che affermare che la ST non sia autentica.